Hvad er et IX diagram og et HX diagram?

Hvad er forskellen på et IX diagram og et HX diagram?

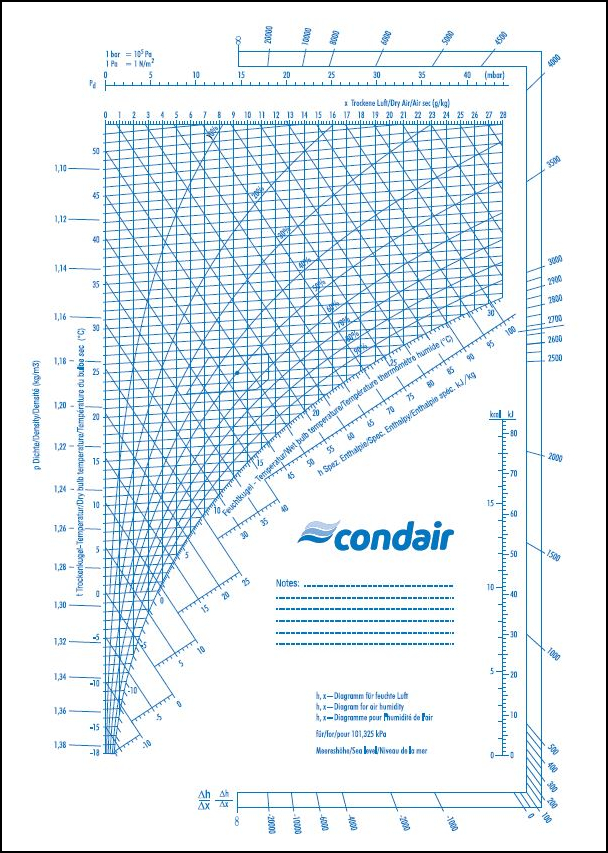
IX diagrammet og HX diagrammet er også kendt som et Mollier diagram. IX diagrammet er illustreret i et vertikalt layout, hvorimod HX diagrammet er vist i et horisontalt layout. 

Diagrammerne viser sammenhængen mellem luftfugtighed, temperatur og energi i luften. Værdierne fra diagrammerne bruges til beregning af korrekt indeklima og luftfugtighed.

På denne side vil vi gå i dybden med HX diagrammet.

Download vores gratis IX diagram og HX diagram

Her kan du downloade de nyeste versioner af IX diagrammet og HX diagrammet gratis. Begge diagrammer er mulige at downloade i en printvenlig version.

Ønsker du at få tilsendt et lamineret IX eller HX diagram? Så er du velkommen til at kontakte os.

Udover de to Mollier diagrammer kan du se teknisk vejrdataberegning ved at download referenceåret her.

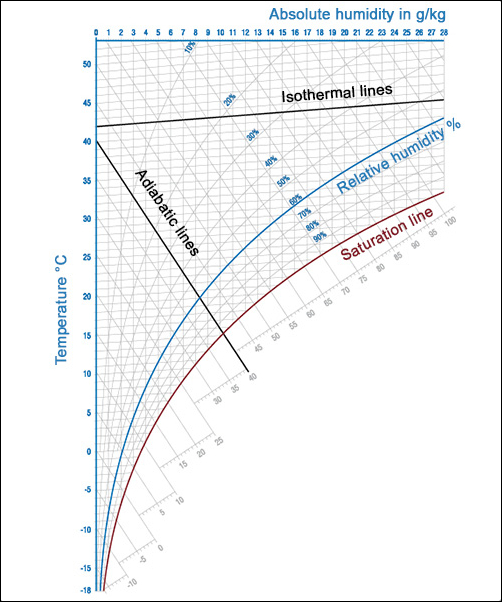
Hvad kan man se i et HX diagram?

Et HX-diagram opstilles som et koordinatsystem med skrå linjer. Denne model blev valgt, da den forøger nøjagtigheden for bedømmelse af størrelsen på området med umættet fugtig luft. For at opstille Molliers foreslåede diagram, roteres x-aksen med uret indtil isoterm t = 0°C ligger horisontalt i området med umættet fugtig luft. Linjerne for konstant-specifik entalpi h løber fra øverst til venstre mod nederst til højre. Linjerne for det konstante vandindhold x løber vertikalt.

Af praktiske årsager løber den horisontale akse, på hvilken vandindhold x påføres, ikke gennem koordinatsystemets udgangspunkt. Vanddampens partialtryk kan angives som en sekundær x-akse, da denne værdi kun baseres på vandindhold x og lufttryk p. Specifik entalpi h påføres på linjer, som løber diagonalt. Opstillinger af kurver foretages for lufttemperatur, tæthed af fugtig luft samt relativ luftfugtighed.

Anvendelse af en rettelinje muliggør nem grafisk illustrering af forholdsændringer - eks. den forholdsændring, der opstår under dampbefugtning. Indekset 1+x indikerer, at fugtig lufts entalpi udgøres af tør lufts entalpi samt vands entalpi. Linjer med ensartede temperarurer (isotermer) stiger en smule i området med umættet luft. Dette ses tydeligt omkring den andel af dampen, hvor entalpi kan registreres. Linjerne bøjer nedad ved mætningspunktet (relativ luftfugtighed = 1), da luft stadig kan indeholde flydende vand i form at små vanddråber (tåge) i tillæg til den maksimalt mulige mængde vanddamp. Isotermerne i tågeregionen fraviger udelukkende fra linjerne for konstant entalpi, som løber igennem mætningspunktet, ved den moderat sporbare entalpi for den tilbageværende mængde vand.

Der er nu kurver af ensartet relativ luftfugtighed i området med umættet luft, som produceres via den jævne adskillelse af isoterm-sektionerne mellem = 0 and = 1. Den relative luftfugtighed formindskes derfor, efterhånden som luften bliver varmere, såfremt vandindholdet x ikke ændrer sig.

Beregning ved hjælp af HX diagrammet

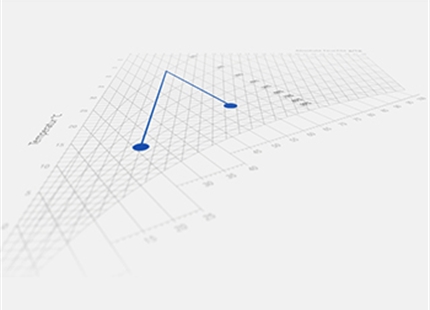
Nedenstående er et eksempel på opvarmningsprocessen for en luftmængde, som ikke udsættes for ændringer i sit dampindhold.

Opvarmning ved konstant absolut luftfugtighed

Opvarmning begynder ved 11°C (punkt 1) og slutter ved 25°C (punkt 2). Den absolutte luftfugtighed x forbliver under denne proces på 4 g/kg. Modsat ændrer den relative luftfugtighed sig fra 50% ved 11°C til 20% ved 25 °C. Entalpi h (1+x) ændres også fra 21.4 kJ/kg til 35 kJ/kg, mens tætheden ændrer sig fra 1.24 kg/m³ til 1.17 kg/m³.

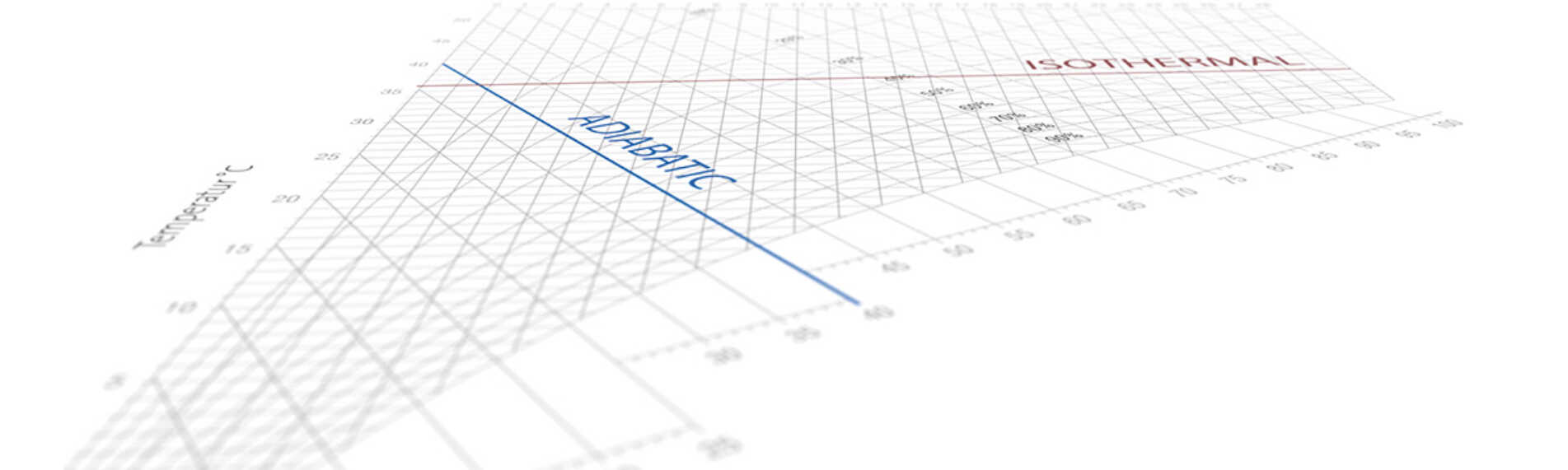
Forstøvning og fordampning af vand (adiabatisk befugtning)

Hvis vand forstøves eller fordampes uden tilførsel af yderligere varme, trækkes den nødvendige energi for fordampningsprocessen fra den omgivende luft. Som følge deraf nedkøles luften. Denne proces er kendt som adiabatisk køling, da køleprocessen sker parallelt med den adiabatiske proces. Rettelinjen ∆h/∆x i h-x-diagrammet viser den præcise retning for nedkølingskurven under befugtning.

Beregning af ∆h/∆x:

∆h           =              kJ/kg
∆x                           kg H₂O/kg tør luft

Her kan du se en video, som forklarer om HX diagrammet